这篇文章覆盖了计算机科学里面常见算法的时间和空间的大 O 复杂度。我之前在参加面试前,经常需要花费很多时间从互联网上查找各种搜索和排序算法的优劣,以便我在面试时不会被问住。最近这几年,我面试了几家硅谷的初创企业和一些更大一些的公司,如 Yahoo、eBay、LinkedIn 和 Google,每次我都需要准备这个,我就在问自己,“为什么没有人创建一个漂亮的大 O 速查表呢?” 所以,为了节省大家的时间,我就创建了这个,希望你喜欢!
首先,我们先弄清楚时间复杂度的概念:
在计算机科学中,时间复杂性,又称时间复杂度,算法的时间复杂度是一个函数,它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。使用这种方式时,时间复杂度可被称为是渐近的,亦即考察输入值大小趋近无穷时的情况。
来看一张表
| f(n) | 释义 |
|---|---|
| O(1) | 常数阶 |
| O(n) | 线性阶 |
| O(log(n)) | 对数阶 |
| O(n²) | 平方阶 |
图例
| 绝佳 | 不错 | 一般 | 不佳 | 糟糕 |
数据结构操作
| 数据结构 | 时间复杂度 | 空间复杂度 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 平均 | 最差 | 最差 | |||||||
| 访问 | 搜索 | 插入 | 删除 | 访问 | 搜索 | 插入 | 删除 | ||
| Array-【数组】 | O(1) | O(n) | O(n) | O(n) | O(1) | O(n) | O(n) | O(n) | O(n) |
| Stack-【栈】 | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Singly-Linked List-【单链表】 | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Doubly-Linked List-【双向链表】 | O(n) | O(n) | O(1) | O(1) | O(n) | O(n) | O(1) | O(1) | O(n) |
| Skip List-【跳表】 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n log(n)) |
| Hash Table-【Hash表】 | - | O(1) | O(1) | O(1) | - | O(n) | O(n) | O(n) | O(n) |
| Binary Search Tree-【二叉查找树】 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) | O(n) | O(n) | O(n) | O(n) |
| Cartesian Tree-【笛卡尔积树】 | - | O(log(n)) | O(log(n)) | O(log(n)) | - | O(n) | O(n) | O(n) | O(n) |
| B-Tree-【多路搜索树】 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Red-Black Tree-【红黑树】 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| Splay Tree-【伸展树】 | - | O(log(n)) | O(log(n)) | O(log(n)) | - | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
| AVL Tree-【自平衡二叉查找树】 | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(n) |
数组排序算法
| 算法 | 时间复杂度 | 空间复杂度 | ||
|---|---|---|---|---|
| 最佳 | 平均 | 最差 | 最差 | |
| Quicksort-【快速排序】 | O(n log(n)) | O(n log(n)) | O(n^2) | O(log(n)) |
| Mergesort-【归并排序】 | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(n) |
| Timsort-【优化版归并排序】 | O(n) | O(n log(n)) | O(n log(n)) | O(n) |
| Heapsort-【堆排序】 | O(n log(n)) | O(n log(n)) | O(n log(n)) | O(1) |
| Bubble Sort-【冒泡排序】 | O(n) | O(n^2) | O(n^2) | O(1) |
| Insertion Sort-【插入排序】 | O(n) | O(n^2) | O(n^2) | O(1) |
| Selection Sort-【选择排序】 | O(n^2) | O(n^2) | O(n^2) | O(1) |
| Shell Sort-【希尔排序】 | O(n) | O((nlog(n))^2) | O((nlog(n))^2) | O(1) |
| Bucket Sort-【桶排序】 | O(n+k) | O(n+k) | O(n^2) | O(n) |
| Radix Sort-【基数排序】 | O(nk) | O(nk) | O(nk) | O(n+k) |
图操作
| 节点 / 边界管理 | 存储 | 增加顶点 | 增加边界 | 移除顶点 | 移除边界 | 查询 |
|---|---|---|---|---|---|---|
| Adjacency list-【邻接表】 | O(|V|+|E|) | O(1) | O(1) | O(|V| + |E|) | O(|E|) | O(|V|) |
| Incidence list-【关联表】 | O(|V|+|E|) | O(1) | O(1) | O(|E|) | O(|E|) | O(|E|) |
| Adjacency matrix-【邻接矩阵】 | O(|V|^2) | O(|V|^2) | O(1) | O(|V|^2) | O(1) | O(1) |
| Incidence matrix-【关联矩阵】 | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|V| ⋅ |E|) | O(|E|) |
堆操作
| 类型 | 时间复杂度 | ||||||
|---|---|---|---|---|---|---|---|
| Heapify | 查找最大值 | 分离最大值 | 提升键 | 插入 | 删除 | 合并 | |
| Linked List (sorted) | - | O(1) | O(1) | O(n) | O(n) | O(1) | O(m+n) |
| Linked List (unsorted) | - | O(n) | O(n) | O(1) | O(1) | O(1) | O(1) |
| Binary Heap-【二叉堆】 | O(n) | O(1) | O(log(n)) | O(log(n)) | O(log(n)) | O(log(n)) | O(m+n) |
| Binomial Heap-【二项堆】 | - | O(1) | O(log(n)) | O(log(n)) | O(1) | O(log(n)) | O(log(n)) |
| Fibonacci Heap-【斐波那契堆】 | - | O(1) | O(log(n)) | O(1) | O(1) | O(log(n)) | O(1) |
大 O 复杂度图表
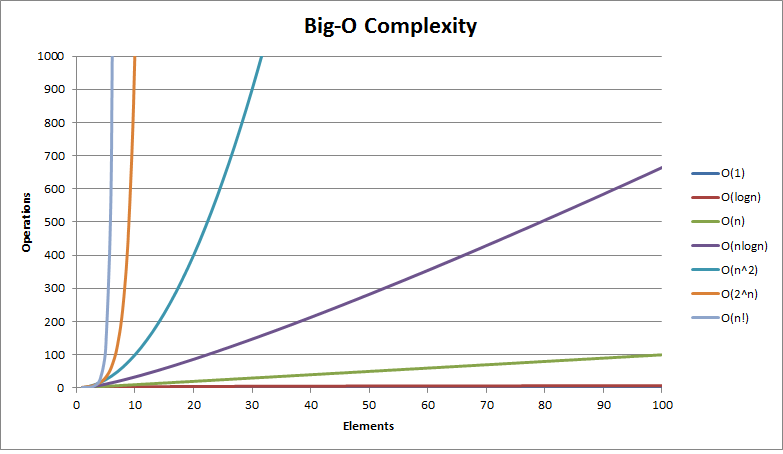
总结 四张常见的时间复杂度的用时如下:
O(1)< O(log(n))< O(n)< O(n^2)
另:编程的世界中还有各种各样的算法,除了上述四种,还有许多不用形式的时间复杂度:
O(n(log(n))),O(n^3),O(m*n),O(2^n),O(n!)


2021-10-03 19:18:52 回复
Remarkable! Its actually remarkable article, I have
got much clear idea regarding from this article.
2021-09-27 16:37:46 回复
I'm really enjoying the theme/design of your blog.
Do you ever run into any browser compatibility problems? A handful of my
blog visitors have complained about my site not working correctly in Explorer but looks great in Safari.
Do you have any suggestions to help fix this issue?
2021-09-27 16:30:13 回复
This design is incredible! You certainly know how to keep
a reader entertained. Between your wit and your videos, I was almost moved
to start my own blog (well, almost...HaHa!) Excellent job.
I really enjoyed what you had to say, and more than that, how you presented
it. Too cool!
2021-09-27 14:45:00 回复
I'm truly enjoying the design and layout of your website.
It's a very easy on the eyes which makes it much
more enjoyable for me to come here and visit more often. Did you hire
out a developer to create your theme? Superb work!
2021-09-27 11:40:53 回复
My brother recommended I might like this website.
He was entirely right. This post truly made my day.
You can not imagine just how much time I had spent for this info!
Thanks!
2021-09-27 09:20:30 回复
Excellent goods from you, man. I've understand your stuff previous to and
you're just extremely fantastic. I really like what you have
acquired here, certainly like what you are saying and the way in which you say
it. You make it entertaining and you still care for to
keep it smart. I can not wait to read far more
from you. This is actually a wonderful site.
2021-09-27 06:52:23 回复
Hello to every one, it's truly a good for me to pay
a visit this web page, it consists of valuable Information.
2021-09-27 05:46:29 回复
I got this website from my pal who informed
me about this website and at the moment this time I am browsing this web site and reading very informative articles or reviews at
this time.
2021-09-27 03:18:39 回复
Hello to every one, it's in fact a good for me to go to see this web
page, it consists of helpful Information.
2021-09-27 03:10:36 回复
Hey I know this is off topic but I was wondering if you knew of any widgets I could
add to my blog that automatically tweet my newest twitter updates.
I've been looking for a plug-in like this for quite some
time and was hoping maybe you would have some experience with
something like this. Please let me know if you run into anything.
I truly enjoy reading your blog and I look forward to your new updates.
2021-09-27 02:07:25 回复
Hmm is anyone else experiencing problems with the images on this blog loading?
I'm trying to figure out if its a problem on my
end or if it's the blog. Any responses would be greatly appreciated.
2021-09-26 21:51:49 回复
This information is priceless. How can I find out more?
2021-09-26 20:56:07 回复
I'd like to thank you for the efforts you've put in writing
this website. I am hoping to check out the same high-grade content by you later on as well.
In truth, your creative writing abilities has encouraged
me to get my own, personal blog now ;)
2021-09-26 20:15:21 回复
I couldn't refrain from commenting. Exceptionally well written!
2021-09-26 11:17:12 回复
I'm now not positive where you're getting your info,
however good topic. I must spend a while finding out much
more or working out more. Thank you for fantastic info I used to be looking for this information for my mission.
2021-09-25 22:59:19 回复
You can definitely see your enthusiasm within the article you write.
The world hopes for even more passionate writers such as you who are not afraid to say how they believe.
All the time go after your heart.
2021-06-16 14:33:40 回复
沙发